Juliaのコードを勝手に最適化してみた

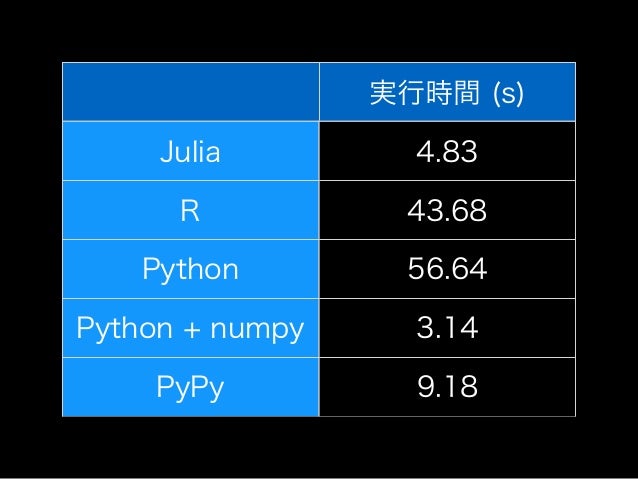
こちらのスライドのパフォーマンスが気になったので、ちょっと速くしてみました。

Juliaのススメ from Ai Makabi

Juliaのススメ

気になったのはコレです。

おかしいっ、我らがJuliaがPython + NumPyに負けるわけないっ。 早速いじってみましょう。

元コードはモンテカルロ法で円周率を計算する次のコードです。

写して実行してみると確かに5秒弱という感じでした。

pi0.jl

tic()
circle_in = 0.0
for i in 1:100000000
    l = (rand()^2 + rand()^2) ^ 0.5
    if l <= 1
        circle_in = circle_in + 1
    end
end
println(4 * circle_in / 100000000)
toc()

~/s/pi-opt $ julia pi0.jl
3.14189192
elapsed time: 4.653206114 seconds

ベンチマークは以下の環境で、3回実行しベストの値を示しています。

julia> versioninfo()
Julia Version 0.3.3
Commit b24213b* (2014-11-23 20:19 UTC)
Platform Info:
  System: Darwin (x86_64-apple-darwin13.4.0)
  CPU: Intel(R) Core(TM) i5-4288U CPU @ 2.60GHz
  WORD_SIZE: 64
  BLAS: libopenblas (USE64BITINT DYNAMIC_ARCH NO_AFFINITY Haswell)
  LAPACK: libopenblas
  LIBM: libopenlibm
  LLVM: libLLVM-3.3

では早速色々と試してみましょう。

1. 関数化

Juliaの最適化は、トップレベルか否かでかなり気合が違います。トップレベルに書かれたコードはあまり最適化が効きません。なので、この計算全体を関数にするだけでかなり速くなることがあります。 試してみましょう。

pi1.jl

function calc_pi()
    circle_in = 0.0
    for i in 1:100000000
        l = (rand()^2 + rand()^2) ^ 0.5
        if l <= 1
            circle_in = circle_in + 1
        end
    end
    println(4 * circle_in / 100000000)
end

@time calc_pi()

~/s/pi-opt $ julia pi1.jl
3.14150504
elapsed time: 1.991970434 seconds (3423756 bytes allocated)

実装を関数でくるんだだけで、倍以上の速さになりましたね。これでPythonには負けないでしょう。

2. 0.5乗の排除

数値計算では0.5乗よりsqrt関数を使ったほうが速いでしょう。 JuliaがベースにしているLLVMにはllvm.sqrt命令がありますし、CPUによっては平方根の計算を効率的に処理できるかもしれません。

diff pi1.jl pi2.jl

--- pi1.jl   2015-01-04 17:08:01.000000000 +0900
+++ pi2.jl  2015-01-04 17:08:05.000000000 +0900
@@ -1,7 +1,7 @@
 function calc_pi()
     circle_in = 0.0
     for i in 1:100000000
-        l = (rand()^2 + rand()^2) ^ 0.5
+        l = sqrt(rand()^2 + rand()^2)
         if l <= 1
             circle_in = circle_in + 1
         end

~/s/pi-opt $ julia pi2.jl
3.141662
elapsed time: 1.381137818 seconds (3386196 bytes allocated)

これだけでも幾分速くなりました。

3. 型合わせ

変数lの比較の両端で型が違うのが気になります。lはFloat64になりますが、Juliaではリテラル1はInt型です。 これを1.0とすることで型を合わせてみましょう。 細かすぎて伝わらないdiffですが、効果はあります。

diff pi2.jl pi3.jl

--- pi2.jl   2015-01-04 17:08:05.000000000 +0900
+++ pi3.jl  2015-01-04 17:35:36.000000000 +0900
@@ -2,8 +2,8 @@
     circle_in = 0.0
     for i in 1:100000000
         l = sqrt(rand()^2 + rand()^2)
-        if l <= 1
-            circle_in = circle_in + 1
+        if l <= 1.
+            circle_in = circle_in + 1.
         end
     end
     println(4 * circle_in / 100000000)

~/s/pi-opt $ julia pi3.jl
3.14178328
elapsed time: 1.236008727 seconds (3374932 bytes allocated)

0.1秒強の改善がありました。一応、足し込む方の+ 1も+ 1.に変えていますが、こちらの効果はあまり無いようでした。

4. 分岐排除

大量に繰り返すループの中で分岐は命取りです。これも削りましょう。 Juliaにはifelseという関数があり、簡単な計算ならこれで分岐を無くすことができます。 ifelseについてはid:yomichiさんの

ifelse() と関数の分離による高速化 -- Base.randn() を題材にして -- - yomichi's blog

が大変参考になります。 今回は1を足すか足さないかという単純な処理ですので、関数評価などのコストを掛けることなくifelseをつかって分岐をなくし効率化できることが期待されます。

diff pi3.jl pi4.jl

--- pi3.jl   2015-01-04 17:35:36.000000000 +0900
+++ pi4.jl  2015-01-04 17:39:37.000000000 +0900
@@ -2,9 +2,7 @@
     circle_in = 0.0
     for i in 1:100000000
         l = sqrt(rand()^2 + rand()^2)
-        if l <= 1.
-            circle_in = circle_in + 1.
-        end
+        circle_in += ifelse(l <= 1., 1., 0.)
     end
     println(4 * circle_in / 100000000)
 end

~/s/pi-opt $ julia pi4.jl
3.14181944
elapsed time: 0.824275847 seconds (3379000 bytes allocated)

1.24s => 0.82sと効果は劇的です。

5. sqrtの排除

よく考えたら1.0と大小比較をしているのでsqrtは要りません。一応これも排除してみましょう。

diff pi4.jl pi5.jl

--- pi4.jl   2015-01-04 17:39:37.000000000 +0900
+++ pi5.jl  2015-01-04 17:44:20.000000000 +0900
@@ -1,7 +1,7 @@
 function calc_pi()
     circle_in = 0.0
     for i in 1:100000000
-        l = sqrt(rand()^2 + rand()^2)
+        l = rand()^2 + rand()^2
         circle_in += ifelse(l <= 1., 1., 0.)
     end
     println(4 * circle_in / 100000000)

~/s/pi-opt $ julia pi5.jl
3.1415418
elapsed time: 0.803608532 seconds (3373236 bytes allocated)

う〜んあんまり速くなりません。これくらいだと実行の度に変わってしまう程度の変動分しかありません。 LLVMは1.0の二乗が1.0であることぐらいは知っていて最適化しているのかもしれませんね。

6. 2乗の排除

もしかしたらx^2よりx*xの方が速いかもしれません。

diff pi5.jl pi6.jl

--- pi5.jl   2015-01-04 17:44:20.000000000 +0900
+++ pi6.jl  2015-01-04 17:49:00.000000000 +0900
@@ -1,7 +1,8 @@
 function calc_pi()
     circle_in = 0.0
     for i in 1:100000000
-        l = rand()^2 + rand()^2
+        x, y = rand(), rand()
+        l = x*x + y*y
         circle_in += ifelse(l <= 1., 1., 0.)
     end
     println(4 * circle_in / 100000000)

~/s/pi-opt $ julia pi6.jl
3.14171304
elapsed time: 0.781361798 seconds (3363408 bytes allocated)

平均的には速くなっている気がしますが、効果はいまいちです。このへんが限界でしょうか。

まとめ

というわけで、4.65s => 0.78sと6倍近い高速化を達成出来ました。 Juliaの最適化は色々とコツが必要ですが、慣れると怪しいところがわかってきます。 最終的なコードは以下の様な感じです。

pi6.jl

function calc_pi()
    circle_in = 0.0
    for i in 1:100000000
        x, y = rand(), rand()
        l = x*x + y*y
        circle_in += ifelse(l <= 1., 1., 0.)
    end
    println(4 * circle_in / 100000000)
end

@time calc_pi()