JuliaによるNelder-Meadアルゴリズムの実装

Optim.jlというJuliaの関数最適化パッケージの出力が気になったのでプルリクエストを投げたら、ちょっと議論になり色々Nelder-Meadアルゴリズムを調べる事になってしまい、その副作用で少し詳しくなったのでJuliaで実装を書いてみました。Optim.jlの実装より高速だと思います。そのパッケージがこちらです: ANMS - Adaptive Nelder-Mead Simplex Optimization

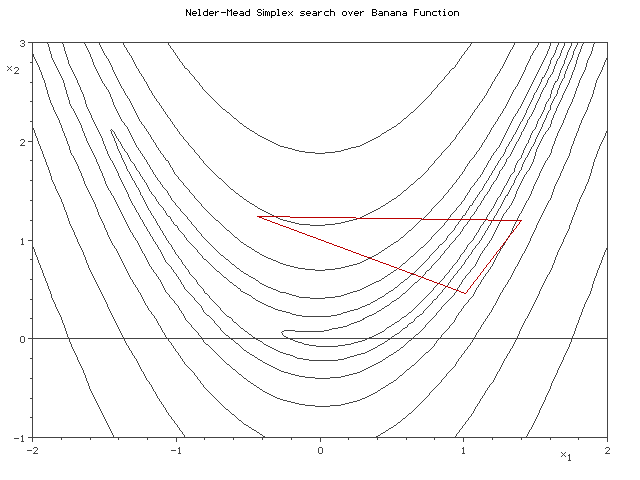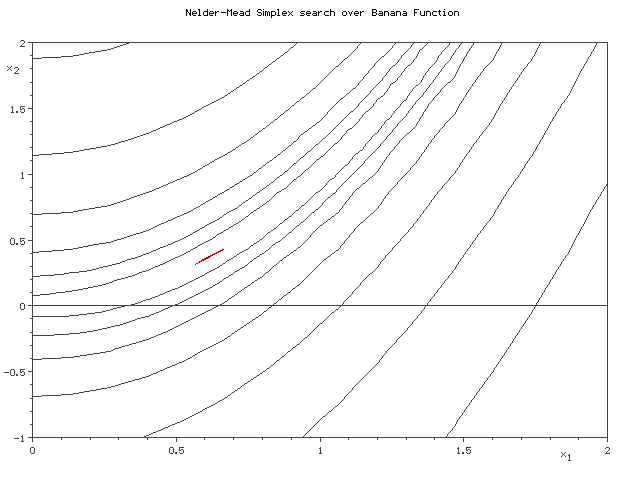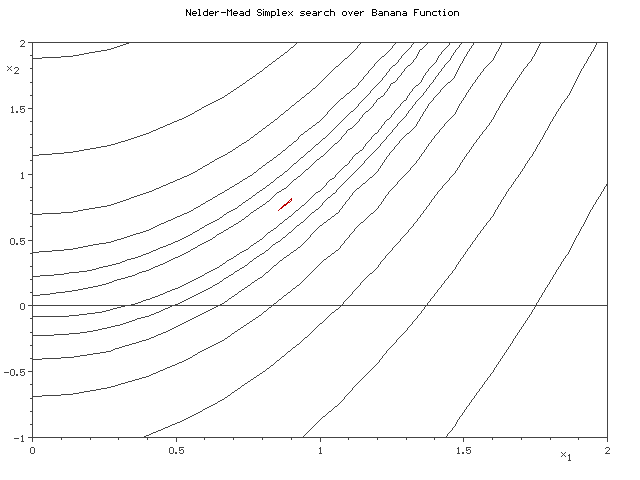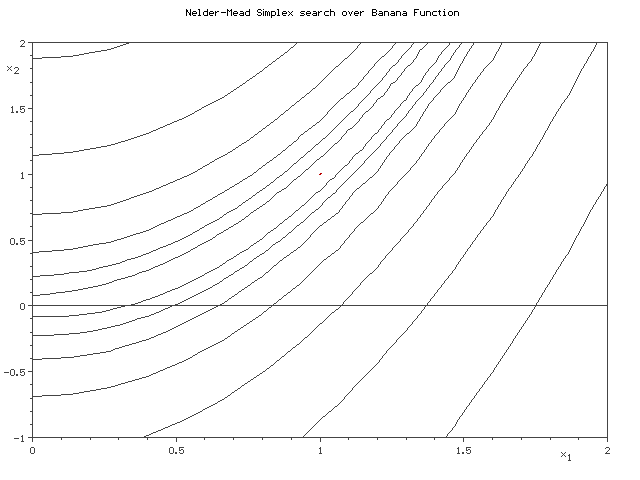
Nelder-Mead法というのは、ご存じの方はご存知のように、n変数の関数の最適化をする際にn+1点からなるsimplex(単体)を変形させながら最小値をgreedyに探索するアルゴリズムです。

アルゴリズム自体は1960年代がある古い古い方法で、数々の亜種が存在します。今回実装したのはそのうちの比較的新しい Adaptive Nelder-Mead Simplex (ANMS) (Gao and Han, 2010) というものです。これは、simplexの変形に関わるパラメータを関数の次元によって変えることで、より関数の評価回数が少なくて済むようになっています。実装自体も最初のパラメータを次元に応じて変える以外はとくに特別なことはしていないため、とても簡単です。

詳細は元論文に譲りますが、simplexの変形は以下の5つからなります。

Relection: $x_r = c + \alpha (c - x_h)$
Expansion: $x_e = c + \beta (x_r - c)$
Contraction:
1. Outside: $x_c = c + \gamma (x_r - c)$
2. Inside: $x_c = c - \gamma (x_r - c)$
Shrink: $x_i = x_l + \delta (x_i - x_l) \quad \text{for} \quad i \ne l$

ここで、 $x_h$ は最大値を取る頂点("h"igh)、 $x_l$ は最小値を取る頂点("l"ow)、 $c$ は最大値を取る頂点を除くsimplexの全頂点の平均("c"entroid)として定義されています。また、 $\alpha, \beta, \gamma, \delta$ は変形のパラメータになります。各頂点の値によって、上の変形のうちのひとつを選択し、新しいsimplexとします。それを繰り返すことで、徐々にsimplexを最小値付近に近づけて行き、ある収束条件や最大反復回数を満たしたところで終了とします。そのsimplexの動きから、アメーバ法などと言われることもあります。