HaskellのFusionがあれば速度と抽象化を両立できる
データの分析をする際には配列やベクトルは欠かせないデータ構造です。 大体どの言語にも大体配列は用意されていて、そこにサンプルのデータ等を入れて統計量を計算したり関数に渡して回帰をしたりするわけです。 ベクトルという単位でデータの塊を扱うものの、実際のアルゴリズムではベクトル内の要素一つひとつを見ていって何か処理をしたり計算をすることが多いでしょう。 その際、命令型言語ではforループを陽に使って要素にアクセスすることになります。
簡単な例を見てみましょう。ベクトルv1とv2の内積を求める関数をC言語で書くと以下のようになります。
function dot(double* v1, double* v2, size_t n) { double s = 0.0; for (int i = 0; i < n; i++) { s += v1[i] * v2[i]; } return s; }
特に難しいところはありませんね:)
ベクトル化された記法
しかし、大きなベクトルに対してこうして陽にループを書くことは、PythonやRではある種の「悪手」であると認識されています。 理由は単純で、PythonやRのインタープリタのループが遅すぎるため、NumPyのようなCやFortranなどで書かれた高速なライブラリに配列(実際にはPythonのオブジェクトが持つメモリ上のバッファへのポインタ)を渡して計算させるのが定石になっています*1。
NumPyやSciPyではこうしたベクトルに対する関数や演算子が大量に用意されており、これらを組み合わせれば、明示的なforループを避けて簡潔に高速な計算ができるようになっているわけです。こうした操作をベクトル化(vectorized)された操作と言われています。
例えば、先程と同様2つのベクトルの内積を計算するならNumPyにnumpy.dot関数が予め用意されています。
import bumpy as np v1 = np.array([1.0, 2.0, 3.0]) v2 = np.array([2.0, 3.0, 4.0]) print(np.dot(v1, v2))
ベクトルの要素ごとの積(*)と総和を求める関数を使えば、内積計算を以下のようにも書くことができます。
def dot(v1, v2): return np.sum(v1 * v2)
分散の計算
こうしたベクトル化された関数を組み合わせて標本分散(不偏分散)を計算してみましょう。 数式での定義は以下のとおりです。
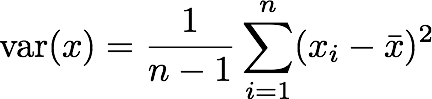
これを単純にNumPyを使ったPythonのコードに写してみましょう。(もちろん、NumPyには分散を計算するnp.var関数が用意されています!)
def var(x): return np.sum((x - np.mean(x))**2) / (np.size(x) - 1)
ベクトル化された関数を使えば、定義式をほとんどそのまま移すだけで、分散を計算する関数が作れました。
しかし、この方法には問題があります。それは、計算の途中に出てくる式の計算のために不要な一時配列が確保され、余計なメモリを食っていることです。
上の例では、x - np.mean(x)では、元の配列xと同じ大きさの配列が確保され、平均からの差分をそこに格納していく形になっています。(x - np.mean(x))**2ではさらに二乗の結果を格納する配列が確保されています。これらの一時的な配列は、本来分散を計算するためにはまったく不要なものです。
内積の例でも、np.sum(v1 * v2)のところでnp.sumに渡す一時ベクトルが新たに作られてしまっています。
def var(x): return np.sum((x - np.mean(x))**2) / (np.size(x) - 1) # ~~~~~~~~~~~~~~ # ^ # ~~~~~~~~~~~~~~~~~~~ # ^ # 余計なベクトルが2個作られている
Pythonのforループは遅くて使えないため、これを回避するためには、CやCythonで陽にループを書くハメになります。
#include <stdlib.h> #include <stdio.h> // Two-pass algorithm: // http://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Two-pass_algorithm double var(double* v, size_t n) { double mean = 0.0; for (int i = 0; i < n; i++) { mean += v[i]; } mean /= n; double ssd = 0.0; for (int i = 0; i < n; i++) { ssd += (v[i] - mean) * (v[i] - mean); } return ssd / (n - 1); }
先ほどのベクトル化された計算と比べると、ループに展開したコードはかなり読みにくく、定義式との対応がわかりづらくなってしまいました。
ちなみに、Juliaでは、マクロを使ってベクトル化された記法からループへと展開するライブラリDevectorize.jlがあります。
fusionを使って宣言的に書き、効率的なコードを吐く
宣言的なベクトル化された記法をしつつ、ループと同等の効率的な実行を可能にするのがfusionです。
fusionでは、中間にできてしまう一時的なベクトルをライブラリによる自動的なコードの書き換え規則とコンパイラによる最適化で排除し、効率的なコードを生成する技術です。
Haskellのvectorパッケージでは、ほとんど意識する必要なくベクトル計算のfusionを行ってくれます。
unboxedな値を格納するベクトルを使うなら、Data.Vector.Unboxedモジュールをインポートして使います。ここでは見た目を簡潔にするため、Preludeの名前が衝突する関数を隠しています。
import Prelude hiding (sum, zipWith) import Data.Vector.Unboxed dot :: Vector Double -> Vector Double -> Double dot v1 v2 = sum $ zipWith (*) v1 v2
v1 * v2ではなくzipWithを使ってる点が若干分かりにくいかもしれませんが、ループを書かずに宣言的に内積が定義できています。それでいて、実はこのdot関数は計算の中間データを保持するベクトルを作っていません!
fusionがどうやって動いているのか
実際にfusionがどのような仕組みになっているか簡単な例で見てみましょう。 ここでは、Stream Fusion - From Lists to Streams to Nothing at Allのサンプルの一部ををGHCで試せるように書いてみます。 これは、stream fusionというfusionの一例です。 vectorパッケージではVector型に対してfusionを行っていますが、ここではリストを使っています。
例えば、map f . map gというコードは関数合成の結合則とstream . unstream ≡ idという関係式から、
map f . map g ≡ (unstream . mapS f . stream) . (unstream . mapS g . stream)
≡ unstream . mapS f . (stream . unstream) . mapS g . stream
≡ ustream . mapS f . mapS g . stream
となります。ここで、streamとunstreamが打ち消しあうことで、リストとStreamの変換が消えますが、これはGHCのrewrite ruleによって実現しています。
さらに、GHCの最適化によりStepの生成も排除され、効率的なコードが吐かれるわけです。
リストに対するstream fusionのより詳しい実装は論文の著者等によるstream-fusionパッケージを参照してください。ただ、最近のGHCは既にリストののfusionをサポートしているため、上のコードやstream-fusionパッケージを使ったものは普通に書いたものと同等のパフォーマンスになりました*2。
分散の計算、再び
分散の計算をvectorパッケージを使って書いてみましょう。 fusionの効果を見るため、わざと関数を分けて定義しています。
import Prelude hiding (sum, length, zipWith, map) import System.Environment (getArgs) import Data.Vector.Unboxed as V -- | pairwise product (.*) :: Vector Double -> Vector Double -> Vector Double x .* y = zipWith (*) x y -- | sample mean mean :: Vector Double -> Double mean v = sum v / fromIntegral (length v) -- | deviations from the mean deviation :: Vector Double -> Vector Double deviation v = map (\x -> x - mean v) v -- | vectorized square square :: Vector Double -> Vector Double square v = v .* v -- | sum of squared deviations from the mean ssd :: Vector Double -> Double ssd = sum . square . deviation -- | unbiased sample variance var :: Vector Double -> Double var v = ssd v / fromIntegral (length v - 1)
このようにかなり宣言的にプログラムを書くことができ、それぞれの関数は単独で使うことも、他の場所で部品として使うこともできるなど再利用性も極めて高いです。Cの方だと可能なのはせいぜい平均値を計算するmean関数をくくりだすくらいでしょうか。
パフォーマンス比較
大きい配列に対してパフォーマンスを比較しみましょう。 長さ100,000,000の配列に対してCのループを使った実装とパフォーマンスを比べてみます。 使用したコードは以下のリンクにあります。 Gist - variance
Haskell: 0.49s user 0.35s system 99% cpu 0.839 total C: 0.48s user 0.33s system 98% cpu 0.815 total
Haskellの実装とCの実装とでほとんど同じ速度がでていますね。Haskellのコンパイルには-fllvmでLLVMのコードを吐くようにすると何割か速くなりました。
本当に一時データが割り当てられていないかも見てみましょう。 Doubleは8byteなので、長さ100,000,000の入力ベクトルに対して800,000,000バイト程度が必要になります。 以下のヒープに割り当てられた領域の大きさからも、不要な配列が割り当てられていないのが分かります。
% ./variance-hs $(cat n) +RTS -s -RTS
800,121,472 bytes allocated in the heap
10,104 bytes copied during GC
44,312 bytes maximum residency (1 sample(s))
21,224 bytes maximum slop
764 MB total memory in use (0 MB lost due to fragmentation)
Tot time (elapsed) Avg pause Max pause
Gen 0 1 colls, 0 par 0.00s 0.00s 0.0001s 0.0001s
Gen 1 1 colls, 0 par 0.00s 0.06s 0.0562s 0.0562s
INIT time 0.00s ( 0.00s elapsed)
MUT time 0.50s ( 0.72s elapsed)
GC time 0.00s ( 0.06s elapsed)
EXIT time 0.00s ( 0.06s elapsed)
Total time 0.50s ( 0.83s elapsed)
%GC time 0.0% (6.8% elapsed)
Alloc rate 1,610,816,342 bytes per MUT second
Productivity 100.0% of total user, 60.0% of total elapsed
新しいfusion
このようにfusionは強力なツールですが、今までのstream fusionにはいくつか限界があります。 最後に、こうした制約を取っ払うために発案された2つのfusionを紹介しましょう。 実装の詳細に関しては、私の能力の限界を超えるため、興味のある方は元の論文を参照してください。
Generalized Stream Fusion
2つのベクトルを結合して新しいベクトルを作りたいことはよくあります。 しかし、既存のstream fusionでは一度に1つづつしか値を取り出せないため、ベクトルを塊として扱うmemcpyのような効率的なコピーができません。 また、同じ理由で複数の値に一気に操作をするSIMD命令も使うことができません。
しかしGeneralized Stream Fusionでは素朴なStreamをより柔軟なBundleという単位にまとめることでこれらの問題を解決してくれます。 2つのベクトルの内積を計算するベンチマークでは、SSEを使うようにしたCのコードと同等かそれ以上の速度を出しています*3。
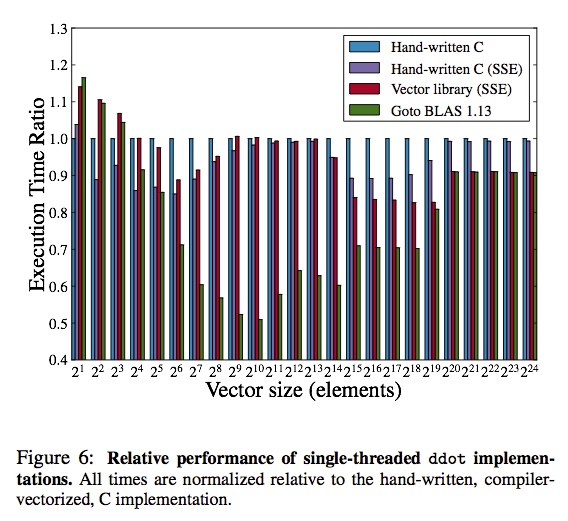
Generalized Stream Fusionでは、既存のHaskellのコードをほとんど変更することなく、合成可能な再利用性を保ったまま高速化できるのが魅力です。 この機能はvectorパッケージ上に実装されています。 現在OpenBLASやEigen3などの数値計算ライブラリと同等のパフォーマンスは出せていませんが、開発が進めばこれらのライブラリに迫るものができるかもしれません。
Data Flow Fusion
もう一つのstream fusionの拡張が、Data Flow Fusionです。 元のstream fusionではベクトルの値を変換して別のベクトルなり集計値を計算する「消費者」は常にひとりだけに限られています。 しかし、1つのベクトルから複数の統計量を計算したりする分岐をしたいことが常です。 大きなベクトルを複数回ループすることはキャッシュの有効利用ができないため、1つのループにまとめるのに比べて不利になってしまいます。
以下のコードは入力ベクトル(vec1)の要素をすべてインクリメントし(vec2)、正数のみを集め(vec3)たものとその中の最大の数をタプルにして返す関数です。
filterMax :: Vector Int -> (Vector Int, Int) filterMax vec1 = let vec2 = map (+ 1) vec1 vec3 = filter (> 0) vec2 n = foldl max 0 vec3 in (vec3, n)
この処理は一度のループで実行可能なはずですが、stream fusionでは1つのfusionにできない処理のようです。また、複数のベクトルに対して同時にループを行うときにループカウンタが重複してしまいレジスタを無駄遣いしてしまうこともパフォーマンスを悪化させてしまいます。
こうした問題をベクトル長の変化やデータフローを解析する高度なfusionによって解決するのがData Flow Fusionです*4。 実装は、Repaの配列に対するGHCの最適化プラグイン(repa-plugin)として提供されているようです。 この最適化により通常のstream fusion(Stream)に比べてdata flow fusion(Flow)では大きく性能が向上し、人間が手でfusionしたCのコード(Hand-fused C)に迫るパフォーマンスの向上を実現しています。
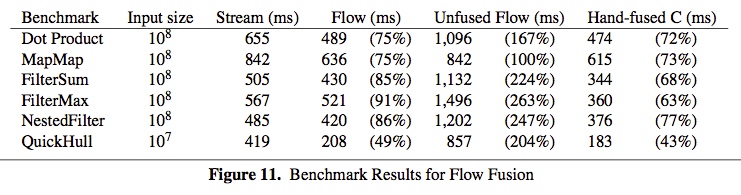
fusionは既に実用的な技術になっており、より強力になったfusionが使えるようになるのもそう遠くないかもしれません。